So, what in the heck is this “Helmholtz Resonator” thing?

*silence*

Heh, yeah, I don’t know either! 

Actually, I just want to start this discussion by stating that the following is simply the method that I use to find how large to make a soundhole. I readily admit that I don’t understand all of the physics and principles behind it all. What I admit that I do know is that this method seems to be better than a completely blind guess. I’ve used it thus far with good results – though that certainly doesn’t mean it is the best or only method to calculate soundhole sizes. 

First, a little background, as well as I understand it…

To begin, a very gifted German scientist and physicist named Hermann von Helmholtz created (among many other things) a device known as a Helmholtz resonator back in the 1860s. It was basically a spherical jug tapering off to a small hole meant to be used for the purpose of studying the resonance of air contained in a cavity. (Similar to the whistling effect when blowing air across the spout of a big glass jug.)

As it has been explained to me, according to Helmholtz’ work, in order to maximize the sound volume of such a resonator, the ideal opening size (in terms of its radius) should be equal to 1/4 of the overall radius of the sphere.

So basically, what we have to do is calculate the total volume inside the psaltery, and then calculate how large a sphere would be that had an identical volume. Then, we simply take the radius of that theoretical sphere, and divide by 4. This number will then be the radius size of the supposedly ideal soundhole – at least in terms of maximum decibel volume.

So, let’s begin with our current psaltery – I hope you’re not afraid of a little math!

Well, this can’t be too tough, it’s a simple triangle, where area is base times height divided by two. 

(B * H / 2)

From there, we just multiply by the depth of the psaltery to get the overall volume. So, taking some inside measurements of the psaltery, I got:

Psaltery length = 18 9/16

Psaltery width = 6 9/16

So, area = ~60.9 in^2

Psaltery depth = 1 1/2

So, total soundbox volume = ~91.36 in^3

Now, to convert this volume measurement into that of a sphere, it gets a little bit tricky. The formula for finding the volume of a sphere is V = 4/3 PI * R^3

Now, rearranging things and solving for R, (this took me a long time to figure out, harkening back to my high-school math days!) we get the following equation:

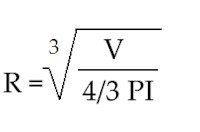
Otherwise written as: R = (V/(4/3*PI))^1/3

So, we take the number we got for the volume of the psaltery, (91.36 in^3) and plug it in as V in our equation.

First we divide it by 4/3 PI, or ~4.1888 and get 21.811

Next, find the cube root, which means 21.811^(1/3)

And we get ~2.79″

So, in a nutshell, the volume of our psaltery is equal to the volume of a sphere with a radius of 2.79 inches. And now for the final payoff, dividing by four to get the size of the soundhole:

So, 2.79/4 = .6975″

So, the ideal soundhole size for this instrument is a circle with a radius of .6975 inches, or a diameter of 1.395″. Overall, a 1 3/8″ (1.375″) hole would do nicely. Now, you’ll notice that I used a triangularsoundhole, so it will help to know the surface area of our ideal hole size, which can be found with the equation for a circle’s area: A = PI * R^2

.6975^2 * PI = ~1.528 in^2

So the number we are shooting for is a surface area of about 1.5 in^2, which can be used for any shape you want to carve into the soundhole. For the triangle, it was pretty simple, as A = B * H / 2, so a simple 1″ x 3″ triangle would have an area of exactly 1.5 in^2 – close enough for me!

Now, I don’t know how accurate any of this all is, but it seems like a good starting point. If you were to start with an instrument with no soundhole, and gradually enlarge it, the sound would get louder and louder. Eventually it would top-out and start getting quieter again. (Imagine a giant 5″ hole in the top of our psaltery!) This is the best way that I know of to find the ideal soundhole size.

One last thought – even if the equation gets us very close to the ideal soundhole size in terms of volume, would this really be ideal? Is volume all that we are concerned with? I’ve heard that smaller soundholes help accentuate the trebles, while larger ones favor the bass end. That is a gross generalization though; you can experiment if you want, and find what you think works best. Me? I’ll just be content with what I’ve got for now.