I should start off by saying that it’s not my intention to speak disparagingly about other bowed psalteries. Certainly there have been many respectable bowed psalteries that have been built with even hitch pin spacing. However, I feel that once you see and understand all the mathematics and the unseen factors that occur behind the stringing of bowed psalteries, you may begin to look at things in a new light.

First off, it will be helpful to gain a basic understanding of the different pitches that make up our common music notes. Any given musical pitch is simply a series of vibrations, measured in how many of these vibrations occur per second, called hertz. The standard that is commonly used today is based on the first A above middle C being tuned to 440 hertz. This is sometimes called “A440 tuning.” Listed below are the notes and frequencies of the musical notes that are used in making our Psimple Psaltery:

Take a look at the lowest note – G4. This is the first G above middle C. (Middle C is not listed, but has a frequency of 261.63 Hz.) Now look at the difference between G4 and the next whole note, A4. It jumps from 392 Hz up to 440 Hz. That’s a jump of 48 Hz.

Next, go up one full octave to G5, and compare G5 to A5. It goes from 783.99 Hz to 880.00 Hz. That’s a jump of….. 48 Hz again? Nope. It’s actually double, at just over 96 Hz difference.

So, what am I trying to say with all of this? The main thing that should be understood is that musical pitches change at an uneven pace. If you ever see a guitar player, look closely at the frets, (the little wire bars that run along the neck of the instrument), and you will notice that the frets are spaced unevenly. The frets at the top are spaced much wider than the frets at the bottom. This is a good way to visualize how the frequency of music changes at an uneven pace.

Now with a bowed psaltery, it is a bit different. On a guitar, the frets must be placed in exactly the right proportions in order for the notes to sound at the right pitch – all the notes are played on that one string, with a fixed amount of tension for all the possible pitches. With a psaltery, we don’t have to get the pins in the exact right place, because if we are off by a little bit, we can compensate by tuning each individual string’s tension up or down so that it is still playing the right note.

So in effect, when we miss this mark, we get just a little bit off from the length that the string really wants to be vibrating at. If we miss the first pin by only 1/8″ from this ideal, it will be no big deal, and probably won’t be noticed. The problem creeps up when we keep on missing this mark, and the errors accumulate and become greater and greater. Soon we’re off by 1/4″ and then by 3/8″ and then before you know it, by the last strings, the spacing is off by several inches.

When strings get stretched too far beyond this ideal, they still sound good, but they tend to break frequently. When strings fall short of this ideal, they give a scratchy or metallic sound which gets worse depending on how far they are away from the ideal.

The general rule of thumb is that this acoustic ideal is about 2/3s of a string’s breaking point; too far over that, and the string is too close to breaking; too far below, and tone will be compromised. Of course, on different instruments, depending on if the strings are plucked or bowed, or very high or very low, these rules can be bent a little. Usually lower strings are more forgiving than higher strings regarding shortness, and bowed strings are much more picky than plucked strings in staying near this number – they need fairly high tension.

Now, let me give some specific, real-world examples and numbers. It will help to show you this graphically. . I’ve taken all the 25 notes listed above for our bowed psaltery project, and charted out two points: 70% of the string’s breaking point (what I consider to be the highest safe point) and 50% of the string’s breaking point (what I consider to be the minimum to have the string still sound acceptable.) Along with this, I’ve charted a hypothetical stringing arrangement that a builder might use (the yellow line).

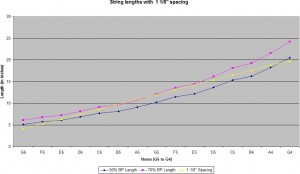Looking at the pink and blue lines – the upper and lower limits of the strings, you will notice sort of a tunnel. In order to create a successful psaltery – that is to say, one that does not have any strings with a dangerously high tension, nor a tension that is too low – I feel that you have to stay within this tunnel. Notice how this tunnel is not straight, but it curves upward? The ideal lengths of strings do not increase evenly, but they get longer at an increasing pace. When we string a psaltery with even spacing, this effectively limits us to drawing a straight line through this tunnel. (Shown above as the yellow line.)

Now, in the above situation, we see our 2-octave psaltery, using pins that are spaced evenly at 1 1/8″ between pins. The middle and long notes around G5 to G4 are great, and everything seems to be going well until we get to the shortest few notes. Notice on G6 and F6 how the yellow line falls below our lower limit? These strings, kept at this length, will sound rather crummy. High notes are especially sensitive to tension – just look at how narrow the tunnel becomes on the left side of the graph! I would even venture to guess that the first 3 highest notes will sound bad, and the fourth will probably be hit-or miss depending on how your bow hits the string. The tension is just too low – the strings need to be longer in order to increase the tension for that note.

Now, let’s take another example, still using even hitch pin spacing:

In the above example, we have kept the longest string (G4) the same length, (this string determines the length of the psaltery, so we won’t be able to change this string unless we physically make the instrument longer), but we have changed the spacing from 1 1/8″ between pins down to 1″. This effectively takes our yellow line and swivels it upward with G4 as our pivot point. Now, the lowest notes will sound good; actually, all the notes should sound good in this example. (Remember that the lowest notes aren’t nearly as picky as the high ones, and we can fudge the rules just a bit on the lower half.)

There is just one problem with this hypothetical psaltery: look at the yellow line over the strings E6 to G5 – busted! B5 is really busted! Many of these strings are very close to their breaking points, approaching 90% of their maximum tension. These strings will really be prone to breaking, especially if you accidentally tune the string a half-step too high, or if there is humid weather – causing the frame to expand. These strings will probably break often (poking your eye out!) and will need to be replaced regularly.

Just looking closely at our arcing tunnel, you may realize that it is not possible to really come up with a stringing scheme that will span the entire distance and still be in the tunnel. Go ahead and try it yourself – enlarge the graph, hold up a sheet of paper or a ruler, and try to make a straight line on your computer monitor that falls within the tunnel. It can’t be done. And this is just with a 2-octave psaltery! Imagine how much the problems would be compounded if you were to continue that narrow tunnel to the left three to six more notes! (And this is exactly what is routinely done.)

Now, let me show you what variable hitch pin spacing does:

The highest notes hug the pink upper limit line, as they are the most sensitive to tension. From there, when we start to get close to the 50% line, we gradually change the spacing. What this does, in effect, is put a nice bend in our yellow line. 

Voila! Our stringing suddenly fits in the tunnel! And not only that, but since we can bend the line in different places, and at different rates, we are also able to break past our 2-octave barrier if we want. (Shown above is the actual spacing used on the psaltery for our project.)

That’s it, in a nutshell. Though I admit, this is a somewhat simplified version, minus all the math and physics! There are a lot more variables that weren’t discussed, but the principles are hopefully clear.

So, for your ears’ sake, for your band-aid box’s sake – consider giving variable hitch pin spacing a chance!